Il Teorema di Bayes e le sue Applicazioni
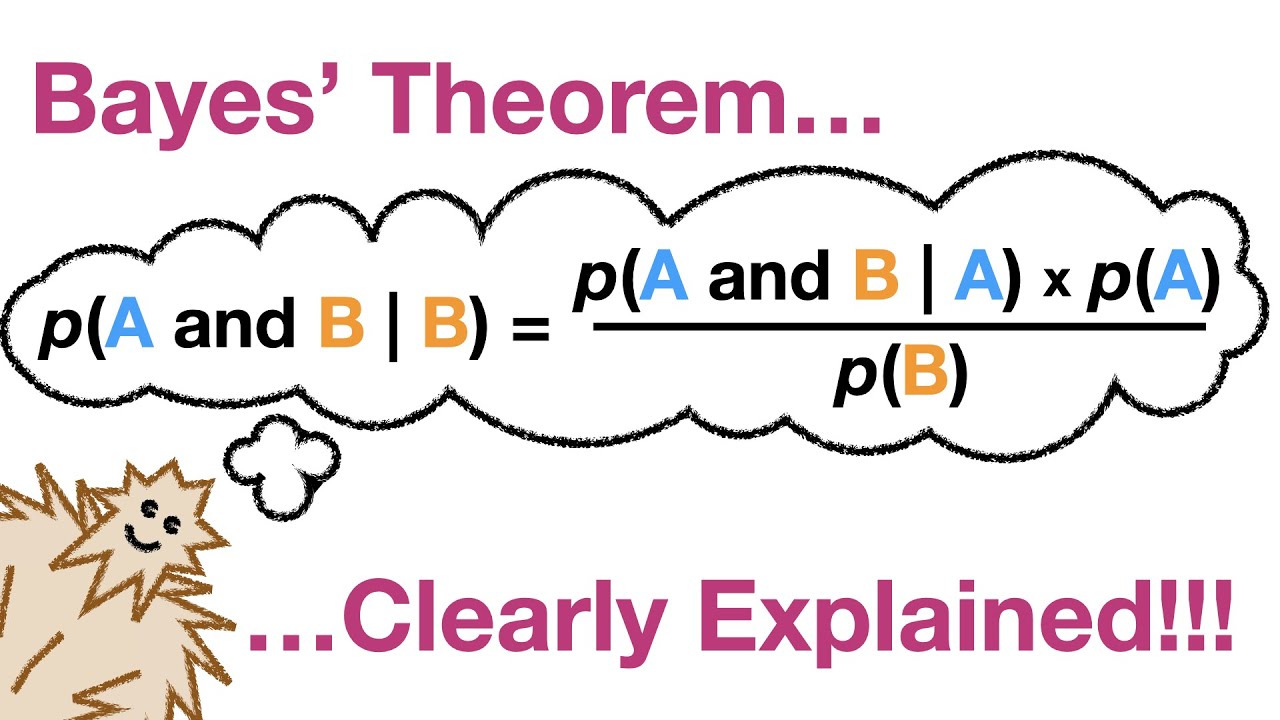
Il teorema di Bayes è uno strumento fondamentale nella probabilità e nella statistica, che ci permette di aggiornare le nostre credenze sulla base di nuove evidenze. In sostanza, il teorema di Bayes ci dice come la probabilità di un evento A, dato che si è verificato un evento B, è correlata alla probabilità di B dato A e alle probabilità a priori di A e B.
Spiegazione del Teorema di Bayes
Il teorema di Bayes può essere espresso dalla seguente formula:
P(A|B) = [P(B|A) * P(A)] / P(B)
Dove:
* P(A|B) è la probabilità di A dato che B si è verificato (probabilità a posteriori).
* P(B|A) è la probabilità di B dato che A si è verificato (probabilità condizionata).
* P(A) è la probabilità a priori di A.
* P(B) è la probabilità a priori di B.
In parole semplici, il teorema di Bayes ci dice che la probabilità di un evento A, dato che si è verificato un evento B, è proporzionale alla probabilità di B dato A, moltiplicata per la probabilità a priori di A, e divisa per la probabilità a priori di B.
Esempi di Applicazioni del Teorema di Bayes
Il teorema di Bayes ha un’ampia gamma di applicazioni in diversi campi, tra cui:
* Medicina: Il teorema di Bayes viene utilizzato per valutare la probabilità che un paziente abbia una determinata malattia, dato il risultato di un test medico. Ad esempio, se un test per il cancro al seno ha un’alta sensibilità e specificità, il teorema di Bayes può essere utilizzato per determinare la probabilità che un paziente abbia il cancro al seno, dato un risultato positivo del test.
* Finanza: Il teorema di Bayes viene utilizzato per valutare il rischio di investimento e per prevedere i rendimenti degli investimenti. Ad esempio, un gestore di fondi può utilizzare il teorema di Bayes per valutare la probabilità di un’azienda di successo, dato il suo stato finanziario attuale.
* Intelligenza Artificiale: Il teorema di Bayes è alla base di molti algoritmi di apprendimento automatico, come i filtri antispam e i sistemi di riconoscimento delle immagini. Ad esempio, un filtro antispam può utilizzare il teorema di Bayes per classificare un’e-mail come spam, dato il suo contenuto e il mittente.
Interpretazioni del Teorema di Bayes
Il teorema di Bayes può essere interpretato in diversi modi, a seconda del contesto e dell’approccio. Due interpretazioni comuni sono:
* Probabilità a priori: La probabilità a priori di un evento è la probabilità che l’evento si verifichi prima di avere qualsiasi informazione aggiuntiva. Ad esempio, la probabilità a priori di ottenere testa lanciando una moneta è 1/2.
* Probabilità a posteriori: La probabilità a posteriori di un evento è la probabilità che l’evento si verifichi, dato che si è verificato un altro evento. Ad esempio, la probabilità a posteriori di ottenere testa lanciando una moneta, dato che si è già ottenuto testa una volta, è 1/2.
Tabella delle Applicazioni del Teorema di Bayes
| Applicazione | Vantaggi | Svantaggi |
|—|—|—|
| Diagnosi medica | Migliora la precisione delle diagnosi | Richiede dati accurati e affidabili |
| Analisi finanziaria | Aiuta a prendere decisioni di investimento più informate | Può essere sensibile ai cambiamenti del mercato |
| Filtraggio antispam | Riduce il numero di e-mail spam | Può bloccare e-mail legittime |
| Riconoscimento delle immagini | Migliora l’accuratezza dei sistemi di riconoscimento delle immagini | Richiede grandi set di dati per l’addestramento |
La Statistica Bayesiana

La statistica bayesiana è un approccio all’inferenza statistica che utilizza il teorema di Bayes per aggiornare le credenze sulla base di nuove evidenze. A differenza della statistica frequentista, che si concentra sulla probabilità di un evento in base a un numero infinito di prove, la statistica bayesiana considera la probabilità come una misura di fiducia in un’ipotesi, basata su informazioni precedenti e su nuovi dati osservati.
Il Concetto di Distribuzione a Priori
La distribuzione a priori è una distribuzione di probabilità che rappresenta la conoscenza o la credenza pre-esistente su un parametro prima di osservare i dati. In altre parole, la distribuzione a priori riflette ciò che sappiamo o crediamo di un parametro prima di raccogliere qualsiasi dato. Ad esempio, se stiamo cercando di stimare la probabilità di successo di una nuova campagna pubblicitaria, la nostra distribuzione a priori potrebbe basarsi su esperienze precedenti con campagne simili o su informazioni sul mercato di riferimento.
Metodi di Inferenza Bayesiana
Esistono diversi metodi per eseguire l’inferenza bayesiana, tra cui:
- Campionamento di Monte Carlo: Questo metodo utilizza la simulazione per generare un numero elevato di campioni dalla distribuzione a posteriori. Questi campioni possono quindi essere utilizzati per stimare la media, la deviazione standard e altre caratteristiche della distribuzione a posteriori.
- Metodo Metropolis-Hastings: Questo metodo è una variante del campionamento di Monte Carlo che utilizza una funzione di proposta per generare nuovi campioni. La funzione di proposta determina la probabilità di accettare o rifiutare un nuovo campione, in base alla sua probabilità a posteriori.
Confronto tra Statistica Bayesiana e Statistica Frequentista
La statistica bayesiana e la statistica frequentista sono due approcci distinti all’inferenza statistica. La statistica frequentista si basa sul concetto di probabilità come frequenza relativa di un evento in un numero infinito di prove, mentre la statistica bayesiana considera la probabilità come una misura di fiducia in un’ipotesi.
| Caratteristiche | Statistica Bayesiana | Statistica Frequentista |
|---|---|---|
| Probabilità | Misura di fiducia in un’ipotesi | Frequenza relativa di un evento |
| Informazione a priori | Utilizzata per aggiornare le credenze | Ignorata |
| Inferenza | Basata sulla distribuzione a posteriori | Basata su test di ipotesi e intervalli di confidenza |
| Interpretazione dei risultati | Probabilità di un’ipotesi data l’evidenza | Probabilità di ottenere i dati osservati se l’ipotesi fosse vera |
- Vantaggi della statistica bayesiana:
- Permette di incorporare informazioni a priori, che possono migliorare la precisione delle stime.
- Fornisce una misura di fiducia in un’ipotesi, che può essere utile per prendere decisioni.
- È flessibile e può essere applicata a una vasta gamma di problemi.
- Svantaggi della statistica bayesiana:
- Può essere computazionalmente costosa, soprattutto per problemi complessi.
- La scelta della distribuzione a priori può influenzare i risultati dell’inferenza.
- Vantaggi della statistica frequentista:
- È relativamente semplice da applicare.
- I risultati sono facilmente interpretabili.
- Svantaggi della statistica frequentista:
- Non permette di incorporare informazioni a priori.
- Può essere sensibile alla dimensione del campione.
Modelli Bayesiani

I modelli bayesiani sono strumenti potenti per l’analisi dei dati che utilizzano il teorema di Bayes per aggiornare le credenze sulla base di nuove informazioni. Offrono un quadro completo per l’inferenza statistica, consentendo di combinare la conoscenza a priori con i dati osservati per ottenere inferenze più accurate e informate.
Tipi di Modelli Bayesiani
I modelli bayesiani si presentano in diverse forme, ciascuna adatta a differenti tipi di problemi e dati. Tra i modelli più comuni troviamo:
- Modelli lineari bayesiani (BLMs): Questi modelli estendono i modelli lineari classici introducendo una distribuzione di probabilità sui coefficienti del modello. Ciò consente di considerare l’incertezza nei parametri e di ottenere inferenze più robuste. Ad esempio, un BLM potrebbe essere utilizzato per modellare la relazione tra l’altezza di un bambino e l’età, considerando l’incertezza nei coefficienti del modello.
- Modelli gerarchici: Questi modelli consentono di analizzare dati strutturati, come quelli raccolti da diversi gruppi o individui. Introducendo livelli gerarchici, è possibile condividere informazioni tra i diversi livelli, migliorando l’accuratezza delle stime. Un esempio di modello gerarchico potrebbe essere utilizzato per analizzare i dati di diverse scuole, condividendo informazioni tra le scuole per ottenere stime più accurate della performance degli studenti.
- Modelli di reti bayesiane (BNs): Queste reti grafiche rappresentano le relazioni di dipendenza tra le variabili di un sistema. Le BNs sono particolarmente utili per analizzare sistemi complessi con molte variabili interdipendenti. Ad esempio, una BN potrebbe essere utilizzata per modellare le relazioni tra i sintomi di una malattia, le cause della malattia e i trattamenti disponibili.
Utilizzo dei Modelli Bayesiani
I modelli bayesiani vengono utilizzati per analizzare i dati e trarre conclusioni attraverso un processo di inferenza bayesiana. Questo processo prevede l’aggiornamento delle credenze a priori sulla base dei dati osservati. Il risultato è una distribuzione di probabilità posteriore che riflette le conoscenze aggiornate.
L’inferenza bayesiana consiste nell’aggiornare le credenze a priori sulla base dei dati osservati, ottenendo una distribuzione di probabilità posteriore che riflette le conoscenze aggiornate.
Applicazioni dei Modelli Bayesiani
I modelli bayesiani trovano applicazione in numerosi settori, tra cui:
- Medicina: I modelli bayesiani vengono utilizzati per analizzare i dati clinici, diagnosticare malattie, prevedere l’esito dei trattamenti e personalizzare le cure.
- Ingegneria: I modelli bayesiani sono utilizzati per la progettazione e l’analisi di sistemi complessi, come quelli utilizzati nell’industria aerospaziale o nell’automazione industriale.
- Economia: I modelli bayesiani vengono utilizzati per prevedere i tassi di interesse, le tendenze del mercato e l’andamento economico.
Software e Strumenti per l’Analisi Bayesiana
Esistono diversi software e strumenti disponibili per l’analisi bayesiana. Tra i più popolari troviamo:
- Stan: Un pacchetto software open-source per l’inferenza bayesiana tramite campionamento MCMC. Stan è noto per la sua flessibilità e la sua capacità di gestire modelli complessi.
- JAGS: Un altro pacchetto software open-source per l’inferenza bayesiana tramite campionamento MCMC. JAGS è più facile da imparare rispetto a Stan, ma può essere meno efficiente per modelli complessi.
- PyMC3: Una libreria Python per l’inferenza bayesiana. PyMC3 è facile da usare e offre un’ampia gamma di funzionalità, tra cui l’inferenza tramite campionamento MCMC e l’approssimazione variazionale.
- BUGS: Un pacchetto software per l’inferenza bayesiana tramite campionamento MCMC. BUGS è stato uno dei primi pacchetti software per l’analisi bayesiana e rimane popolare per la sua semplicità e affidabilità.
Bayesian inference, a powerful tool for analyzing data, encourages a constant updating of beliefs based on new evidence. This process of refinement, akin to the journey of self-discovery, is closely intertwined with the concept of autonomy , where individuals are empowered to shape their own understanding and navigate the world with a critical and independent mind.
By embracing the Bayesian approach, we cultivate an openness to new information and the freedom to evolve our perspectives, ultimately fostering a deeper sense of autonomy in our intellectual pursuits.
